第六讲
如何在噪声的存在中进行准确的状态估计。
1. 状态估计问题
对机器人的状态估计,就是求已知输入数据 u 和观测数据 z 的条件下,计算状态 x 的条件概率分布:
$$
\text P(x\mid z,u)
$$
如果只考虑 u ,根据贝叶斯公式:
$$
P(x|z)=\frac{P(z|x)P(x)}{P(z)}\propto P(z|x)P(x)
$$
后验概率正比于似然先验,但通常也没有先验知识,于是成了求解 $\arg \max P(z|x)$, 似然指的是“在当前的位姿下,可能产生什么样的数据”,最大似然估计就是“在什么样的位姿下,最可能观测到现在观察到的数据”。
SLAM 模型由两个观测方程(运动和观测)组成:
$$
x_k=f(x_{k-1},u_k)+w_k\
z_{k,j}=h(y_i,x_k)+v_k
$$
噪声项满足零均值的高斯分布,对于观测方程:
$$
P(z_{j,k}\mid x_k,y_j)=N(h(y_i,x_k),Q_{k,j})
$$
通常使用最小化负对数的方式来求高斯分布的最大似然。
求解优化问题使用 最速下降法 和 高斯牛顿法:
g2o 框架
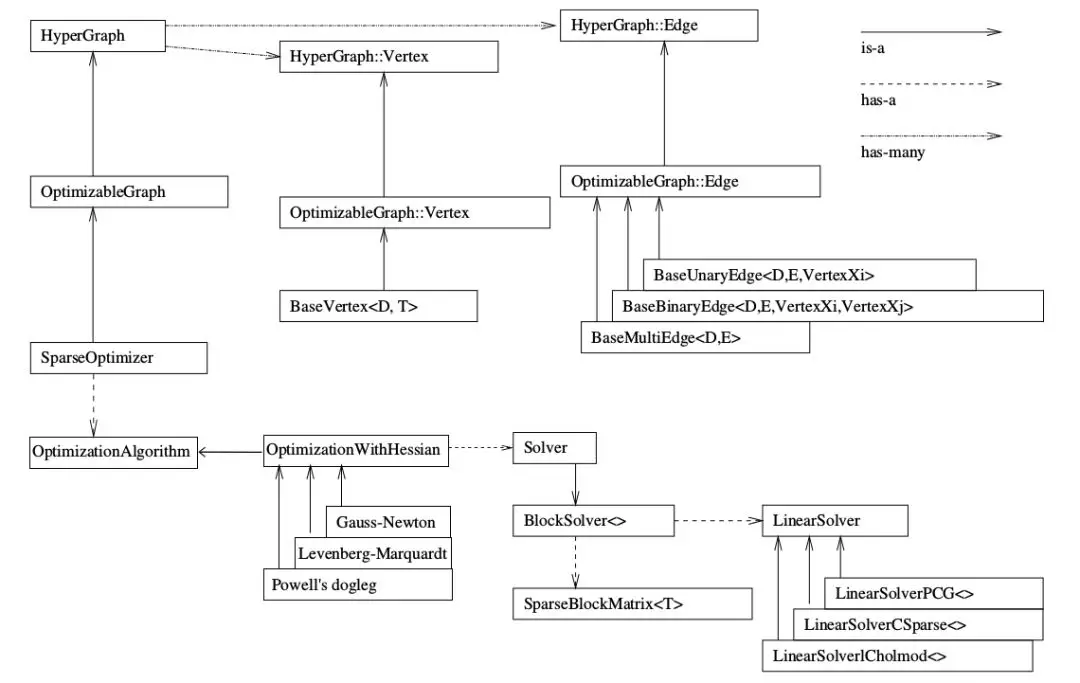
核心位置是 SparseOptimizer ,它包含一个优化算法 OptimizationAlgorithm 通过 OptimizationWithHessian 实现(策略可以是GN、LM等),Solver 是一个求解器,一个是SparseBlockMatrix ,用于计算稀疏的雅可比和Hessian矩阵;一个是线性方程的求解器(LinearSolver),它用于计算迭代过程中最关键的一步HΔx=−b。
图优化
一种把优化问题表示为图的形式,一个图包含若干个顶点(Vertex)和边(Edge),用顶点表示优化变量边表示误差项,对于一个非线性最小二乘问题,可以构建与之对应的一个图。
使用g2o的前提就是将曲线拟合问题抽象为图优化,节点为优化变量,边为误差项,使用g2o的步骤是:
- 定义顶点和边的类型;
- 构建图;
- 选择优化算法;
- 调用 g2o 框架。