第四讲
假设某个时刻相机的位姿是 T ,它观察到一个在世界坐标系的一个空间点 p,观测数据为 z。这时,有
$$
z=Tp+w
$$
观测误差定义为:
$$
e=z-Tp
$$
假设有 N 个这样的三维点和观测值,目标就是寻找一个最佳的位姿使得整体误差最小化:
$$
\min_TJ(T)=\sum^N_{i=1}|z_i-Tp_i|^2_2
$$
求这个问题就是 求目标函数 J 对于变换矩阵 T 的导数。
李群和李代数
三维旋转矩阵构成了特殊正交群,变换矩阵构成了特殊欧式群。
群 是一种集合加上一种运算的代数结构。
旋转矩阵集合和矩阵乘法构成群,变换矩阵和矩阵乘法也构成群。
李群 是指具有连续性质的一类群,特殊正交群、特殊欧式群在实数空间上是连续的(刚体能够连续地在空间中运动),它们都是李群。
李代数 :每个李群都有对应的李代数,用于描述李群的 局部性质。李代数由一个集合,一个数域和一个二元运算组成。二元运算称为李括号,李括号表达了两个元素的差异 ($\forall x\in \mathbb{V},[X,X]=0$)。
特殊正交群 SO(3) 对应的李代数是定义在 $\mathbb{R}^3$ 上的向量,记作 φ ($\phi^\wedge=-(\dot R(t) R(t)^T)^T$)。
特殊欧式群 SE(3) 对应的李代数中每个元素是一个六维向量,前三维表示平移,后三维表示旋转,记作
$$
\xi=\begin{bmatrix}\rho\\ \phi \end{bmatrix}\in \mathbb{R}^6
$$旋转矩阵的微分 $\dot R$ 是一个反对称矩阵左乘它本身,$\dot R(t) =\phi(t)^\wedge R(t)$。
反对称矩阵 ($A^T=-A$)特点是 对角线元素都是 零。3 × 3 的反对称矩阵只需用三个元素表示(自由度是3),可以用于建立三维向量和三维矩阵的关系。
假设有一个反对称矩阵 A :
$$
A=\begin{bmatrix}0 &-a_3 &a_2\\ a_3 &0 &-a_1\\ -a_2 &a_1 &0\end{bmatrix}
$$
定义一个三维向量:$a=[a_1,a_2,a_3]^T$,然后用 wedge 符号表示向量 a 和矩阵 A 之间的关系:
$$
a^\wedge=A
$$
于是
$$
\dot R(t) =\phi(t)^\wedge R(t)=\begin{bmatrix}0 &-\phi_3 &\phi_2\\ \phi_3 &0 &-\phi_1\\ -\phi_2 &\phi_1 &0\end{bmatrix}R(t)
$$
指数与对数映射
李群空间的任意一个旋转矩阵R都可以用李代数空间的一个向量的反对称矩阵指数来近似。
$$
R(t)=\exp(\phi^\wedge_0t)
$$
旋转矩阵的导数可以由其对应的旋转向量指定,指导如何在旋转矩阵中进行微积分运算。
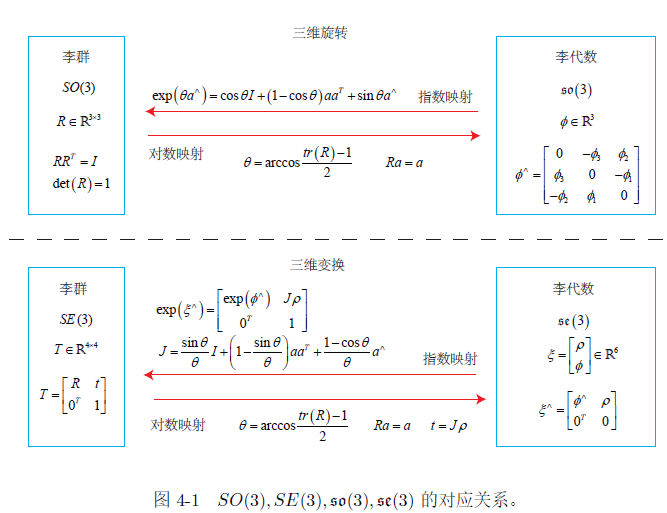
so(3) 是旋转向量组成的空间,而指数映射是罗德里格斯公式,通过这个公式将 so(3) 中任意一个向量对应到了位于 SO(3) 中的旋转矩阵,对数映射是反变换。
李代数求导与扰动模型
两个矩阵指数之积,会产生一些由李括号组成的余项。但是李代数是小量时,二次项可以忽略。利用这个关系有,一个旋转矩阵 $R_2$ 左乘一个微小的旋转矩阵 $R_1$ ,可以近似的看作在原有李代数 $\phi_2$ 加上了 $J_l(\phi_2)^{-1}\phi_1$ (称为 BHC 近似,右乘是 $J_r(\phi_1)^{-1}\phi_2$)。
SO(3) 在李代数的求导
在 SLAM 中,对相机位置和姿态是由 SO(3) 上的旋转矩阵或者 SE(3) 上的变换矩阵描述的。通常会构建与位姿有关的函数,然后讨论该函数关于位姿的导数,以调整当前的估计值。使用李代数解决求导的思路分为两种:
- 李代数表示姿态,然后根据李代数加法对李代数求导。
- 对李群 左乘 或 右乘 微小扰动,然后对该扰动求导。
扰动模型的计算较为简单,假设对一个空间点 p 进行了旋转得到了 Rp ,左扰动 $\Delta R$ 对应的李代数为 $\phi$ ,然后对 $\phi$ 求导:
$$
\begin{align}\frac{\partial (Rp)}{\partial\phi}&=
\lim_{\phi\rightarrow 0}\frac{\exp(\phi^\wedge)\exp(\Phi^\wedge)p-\exp(\Phi^\wedge)p}{\phi}\\
&\approx \lim_{\phi\rightarrow 0}\frac{(1+\phi^\wedge)\exp(\Phi^\wedge)p-\exp(\Phi^\wedge)p}{\phi}\\
&=\lim_{\phi\rightarrow 0}\frac{\phi^\wedge\exp(\Phi^\wedge)p}{\phi}=\lim_{\phi\rightarrow 0}\frac{\phi^\wedge Rp}{\phi}\\
&=\frac{-(Rp)^\wedge\phi }{\phi}=-(Rp)^{\wedge}\end{align}
$$